Divide-and-conquer 와 Dynamic Programming 비교

---

Divide-and-conquer

정의: ‘나누고 정복한다’는 의미로 크고 복잡한 문제를 보다 해결하기 쉬운 단위로 나눠서 해결한 후 다시 합치는 알고리즘이다. Recurrence function으로 구현 표현 가능하고 자기 자신보다 작은 문제로 나누다가 Base case에 도달하면 리턴한다.

예시: 가장 대표적인 Divide-and-conquer(이하 D-and-C)의 예시로 정렬 알고리즘 중에 mergesort가 있다. 대부분의 sorting 알고리즘들(insertion, selection 등)의 time complexity는 O(n^2)인데 비해, D-and-C의 개념을 사용한 merge sort는 time complexity가 O(nlogn)로 훨씬 좋은 효율을 보인다.

Dynamic Programming

정의: 큰 문제를 작은 문제로 나누어 푸는 알고리즘이다. Divide-and-conquer와 비슷하지만 작은 문제의 중복이 일어나지 않는다는 점에서 다르다. Dynamic Programming(이하 DP)으로 풀 수 있는 문제의 전제 조건은 해당 문제가 Optimal Substructure를 가지고 있는지 여부이다. Optimal substructure란 문제의 궁극적인(최적의) 솔루션이 더 작은 문제의 최적의 솔루션들로 이루어져있다는 개념이다. 즉, 작은 문제부터 해결해나가지만 작은 문제 중의 최적의 솔루션이 큰 문제의 솔루션에도 쓰인다는 것이다. 이러한 구조를 가지고 있는 문제는 DP로 해결할 수 있다.

예시: 가장 대표적인 DP 문제로 Matrix Chain Multiplication(MCM)문제와 Longest Common Subsequence(LCS)문제가 있다. 두 문제 모두 특정 부분까지의 최적의 솔루션을 메모해 놓았다가 그 다음 부분의 최적의 솔루션을 결정하는 방식으로 Optimal Substructure를 가지고 있기 때문에 DP를 적용할 수 있다.

Divide-and-conquer vs Dynamic Programming

두 문제 모두 문제의 해결 방식이 큰 문제를 작은 문제로 나누는 방식이라는 점에서 공통점이 있지만 DP의 경우 작은 문제부터 풀고 작은 문제의 솔루션을 메모해 놓았다가 큰 문제에서 작은 문제의 솔루션을 그대로 가져다 쓰는 방식인 것에 반해 D-and-C의 경우 작은 문제를 풀 때 전에 이미 풀었던 문제이더라도 다시 푸는 방식이기 때문에 같은 계산 작업이 많은 문제의 경우 DP가 D-and-C보다 더 유리하다고 할 수 있다. 일반적으로 D-and-C는 위에서부터 아래로 내려오는 Top-down 방식이지만 DP의 경우 Bottom-up방식(Top-down도 가능)이다.

코드 예시

아래는 nCr을 D-and-C와 DP로 각각 풀고 걸리는 시간을 테스트 한 코드이다

#include <stdio.h>
#include <time.h>

int RecursiveSolution(int n, int k);
int DpSolution(int n, int k);


int main(){
    int n, k;
    int RecursiveAnswer, DpAnswer;

    clock_t start, end;
    float rs1, rs2;

    printf("\n***** Combination Calculation Problem(nCk) *****\n\n");
    printf("Enter number for n : ");
    scanf("%d", &n);
    printf("Enter number for k : ");
    scanf("%d", &k);

    start = clock();
    RecursiveAnswer = RecursiveSolution(n,k);
    end = clock();
    rs1 = (float)(end-start)/CLOCKS_PER_SEC;

    start = clock();
    DpAnswer = DpSolution(n,k);
    end = clock();
    rs2 = (float)(end-start)/CLOCKS_PER_SEC;

    printf("\n> nCk with Recursive Solution         : %d", RecursiveAnswer);
    printf("\n> nCk with DP Solution                : %d", DpAnswer);
    printf("\n> Elapsed time for Recursive Solution : %.6f", rs1);
    printf("\n> Elapsed time for DP Solution        : %.6f\n\n", rs2);
    return 0;
}

int RecursiveSolution(int n, int k) {

    if(k == 0 && n >= 0) return 1; 
    // case 1
    else if(n == 0 && k > 0) return 0;
    // case 2
    else if(n == k) return 1;
    // case 3
    else /* if(n > 0 && k > 0) */ return RecursiveSolution(n-1, k-1) + RecursiveSolution(n-1, k);
    // case 4
}

int DpSolution(int n, int k){

    int arr[k+1][n+1];

    for(int p = 0 ; p <= n ; p++) {
        arr[0][p] = 1;
    } // case 1

    for(int p = 1 ; p <= k ; p++) {
        arr[p][0] = 0;
        // case 2
        arr[p][p] = 1;
        // case 3
    }

    for(int i = 2 ; i <= n ; i++) {
        for(int j = 1 ; j <= k ; j++) {
            if(i > j) arr[j][i] = arr[j-1][i-1] + arr[j][i-1];
            else continue;
        }
    } // case 4
    
    return arr[k][n];
}

코드 실행 결과

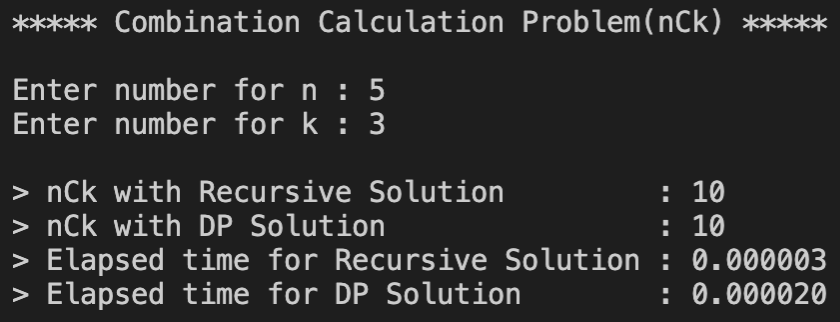
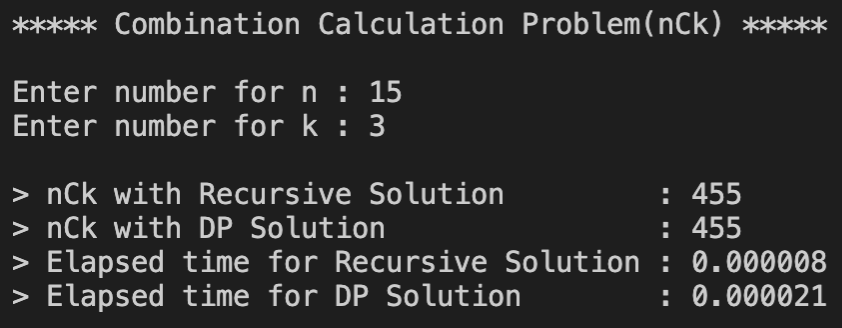
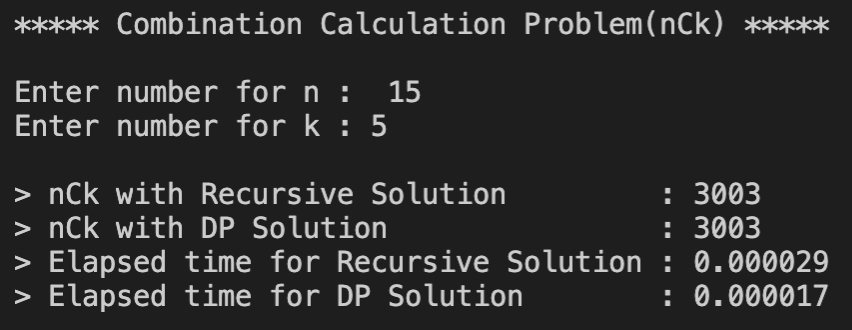
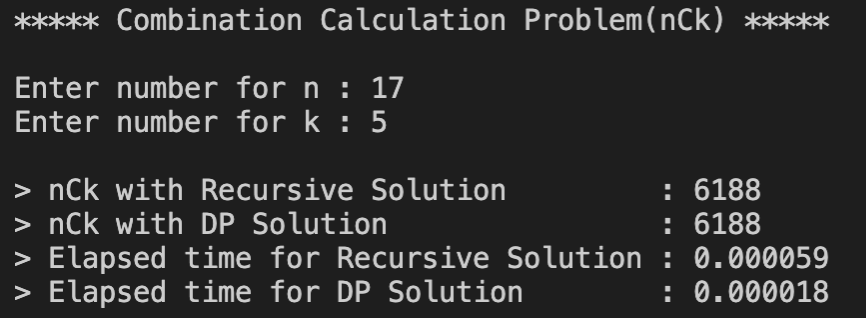
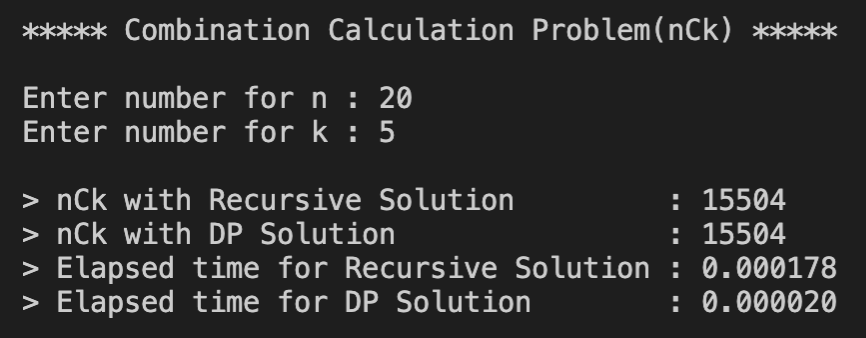
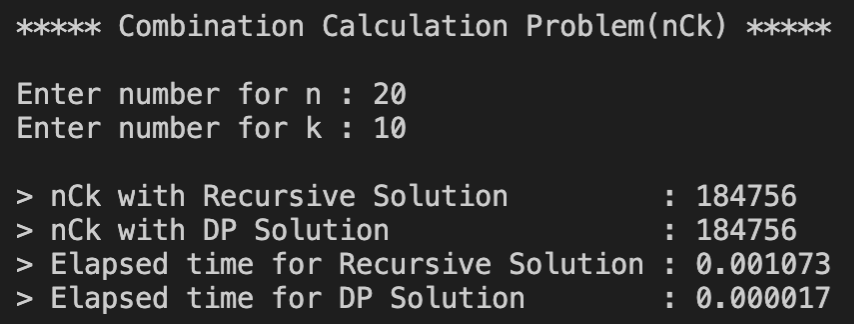
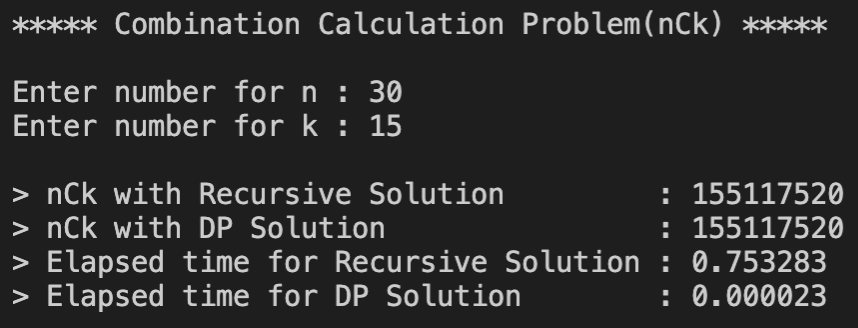
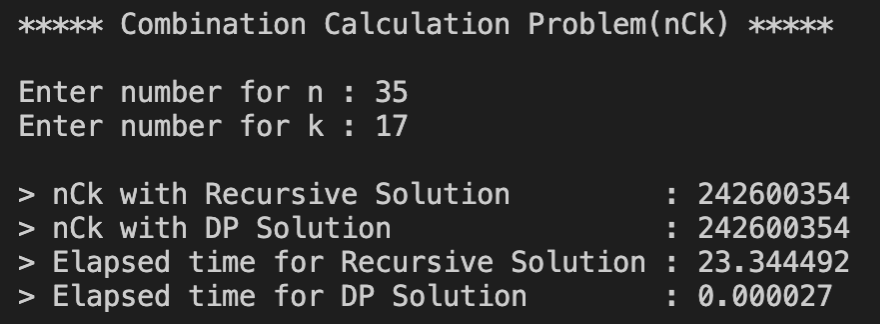
Input이 적을 때는 D-and-C가 더 시간이 적게 걸리다가 Input이 커지기 시작하자 DP는 시간의 변화가 크게 없는 반면에 D-and-C는 시간이 기하급수적으로 늘어나면서 나중에는 큰 Input에는 거의 작동할 수 없는 수준에 이르렀다. 조합을 찾는 공식 nCr = n!/r!(n-r)! 특성상 D-and-C는 같은 문제를 수십, 수백번 풀게 되는 반면에 DP는 문제의 해답을 배열에 저장해 놓았다가 답만 가져오기 떄문에 초반에는 D-and-C보다 시간이 조금 더 걸렸지만 숫자가 커지면 커질수록 유리하다는 것을 확인할 수 있다.