[백준 2644번] 촌수계산 (DFS)

문제 화면

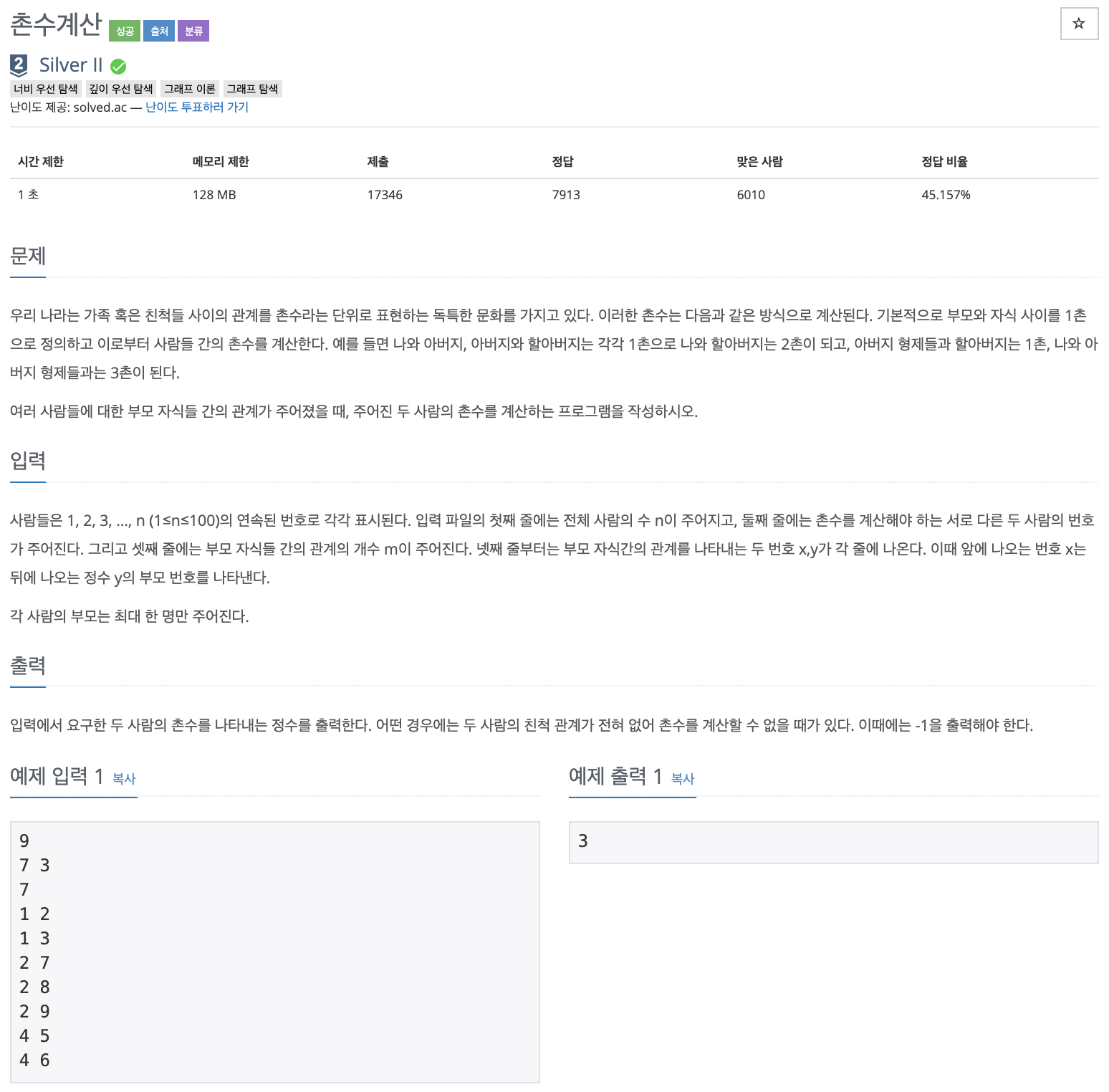
문제 링크 : https://www.acmicpc.net/problem/2644

문제 풀이

이 문제는 tree가 주어지고 A와 B 노드 사이의 최단거리를 구하는 문제이다. 이 문제가 tree구조인 이유는 족보이기 때문에 cycle이 없고 부모 자식간에 연결된 관계가 주어지기 때문이다. 물론 문제에서 한개의 tree만 준다는 보장은 없다. 만약 A노드와 B노드가 연결되어 있지 않은 각각 다른 tree에 존재할 경우 (위의 문제의 설명에서 두 사람의 친척 관계가 전혀 없어 촌수를 계산할 수 없는 경우) ‘-1’을 출력해주면 된다.

구상

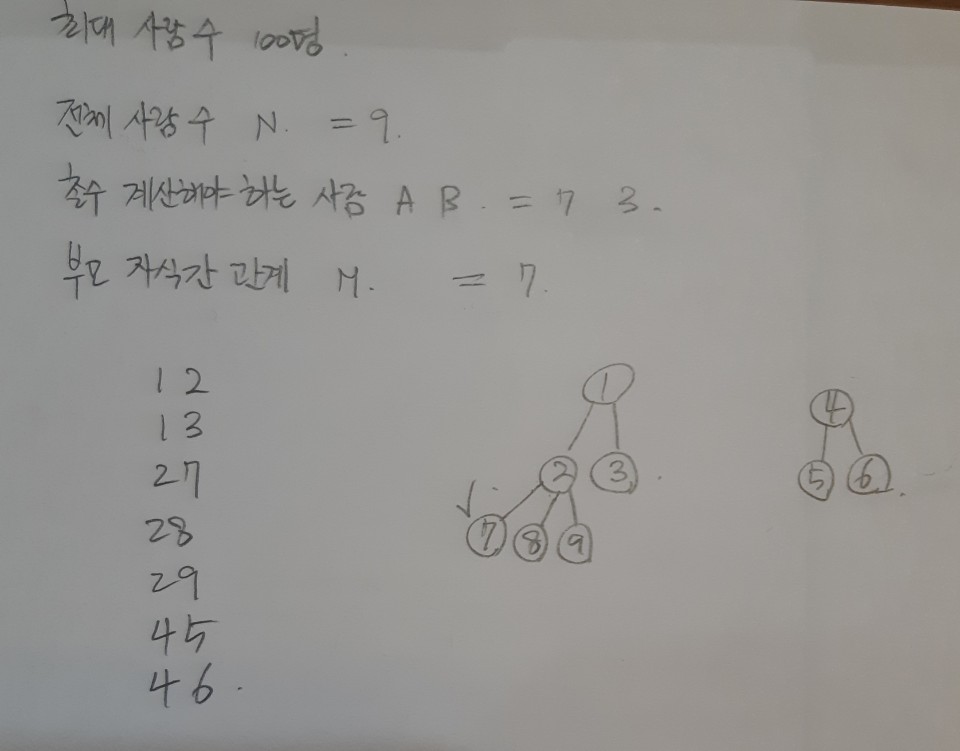
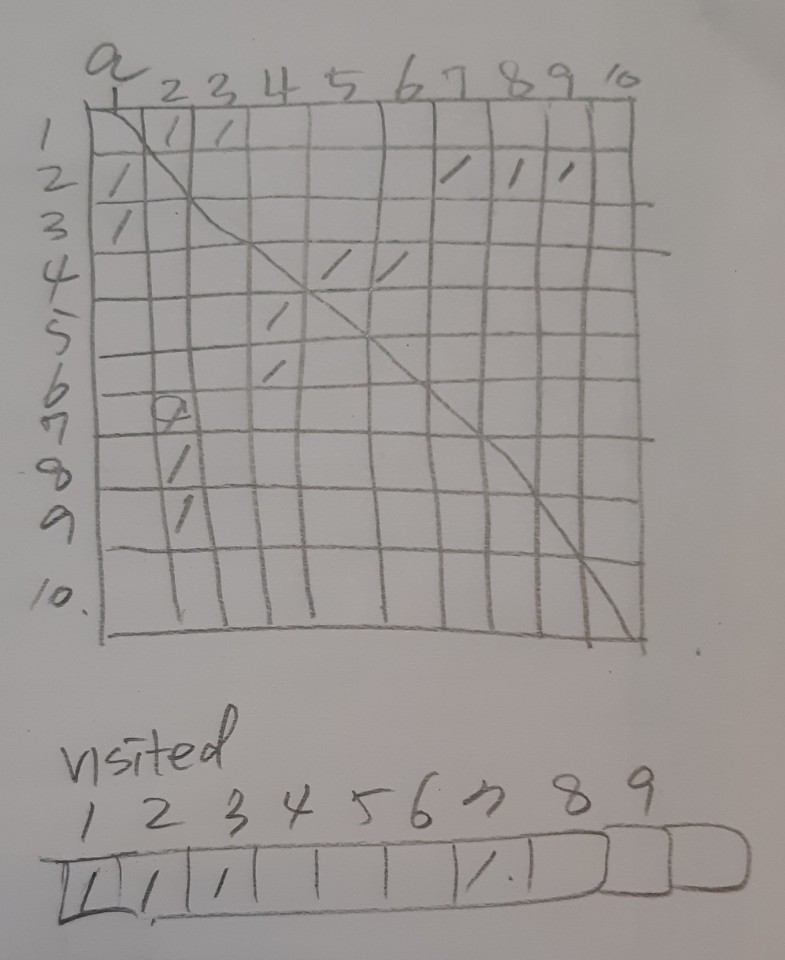
문제에서 주어지는 부모와 자식간의 관계를 2차배열로 저장한다. tree이기 때문에 edge의 방향이 없는 것을 고려하여 부모와 자식의 관계가 주어지면 양방향을 저장한다. 예를들어 배열 이름이 A이고 문제에서 7과 3이 주어지는 경우 A[7][3] = 1, A[3][7] = 1로 저장한다. 관계가 없는 경우 모두 0으로 초기화 한다. 그리고 재귀함수를 통해 시작노드부터 목표 노드까지 찾아가는데 이때 각 노드별로 연결된 노드가 있는지, 그리고 연결된 노드가 방문하지 않은 노드인지 확인하면서 모든 노드를 돌 수 있도록 한다. 각 노드를 방문할 때는 count를 +1씩 최신화 해주면서 방문한 노드가 목표노드인 경우 count값을 정답으로 출력할 수 있도록 한다.

제출 코드

#include <iostream>
#include <vector>

using namespace std;

vector<vector<int>> v(101,vector <int>(101,0)); // 관계 저장 벡터 
vector<int> visited(101,0); // 방문여부 확인 벡터 
int answer = -1; // 출력할 정답(촌수) 저장 변수 
bool answerFound = false;
int N;

void dfs(int start, int target, int count) {
  visited[start] = 1;
  if(start == target) {
    answer = count;
    answerFound = true;
    return;
  }
  
  for(int i = 1 ; i <= N ; i++) {
    if(v[start][i] == 0) continue; // 아무 관계가 없는 경우 다음 사람(노드) 건너 뛰어라 
    else if(v[start][i] == 1 && visited[i]) continue; // 연결이 되었지만 이미 방문이 끝난 경우 건너뛰어라 

    else {
      dfs(i, target, count + 1);
      if(answerFound) break;
    }
  }
  return;
}

int main() {
  int x, y;
  int A, B, M;

  scanf("%d", &N);
  scanf("%d %d", &A, &B);
  scanf("%d", &M);
  
  for(int i = 0 ; i < M ; i++) { // 주어진 부모 자식간의 관계 개수만큼 입력받아라 
    scanf("%d %d", &x, &y);
    v[x][y] = 1;
    v[y][x] = 1;
  } // 관계 선 연결

  dfs(A, B, 0);

  cout << answer;

  return 0;
}

결론

주어지는 문제가 트리구조인 것을 알아내고 2차 배열로 트리의 구조를 저장한 이후에 DFS 알고리즘을 통해 풀 수 있는 문제이다. 최단거리를 알아내는게 핵심이기 때문에 BFS에도 최적화 되있는 문제이다. 재귀함수가 직관을 필요로 하는 부분이기 때문에 이 문제를 통해 재귀함수를 코드로 구현하는 연습을 할 수 있어서 좋았다.